11.玻尔兹曼分布
玻尔兹曼分布:
在物理学(特别是统计力学)中,麦克斯韦 - 玻尔兹曼分布是以詹姆斯·克拉克斯·马克斯韦尔和路德维希·波兹曼命名的特定概率分布。
这是第一次定义,并且用于描述颗粒速度在理想化的气体,其中所述颗粒的固定容器内自由移动,而不会彼此互动,除了非常简短的碰撞,其中它们与彼此或与它们的热环境交换能量和动量。在该上下文中,术语“颗粒”仅指气态颗粒(原子或分子),并且假设颗粒系统已达到热力学平衡。[1] 这种粒子的能量遵循所谓的 麦克斯韦 - 玻尔兹曼统计通过将粒子能量与动能等同来推导出速度的统计分布。
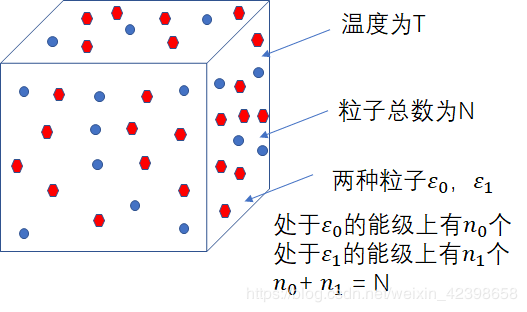
在一个封闭的空间中,温度为T,里面只有两种能级 $ \large \varepsilon _{0},\varepsilon _1 $,粒子的总数为N,且两种能级对应的个数分别为:$ \large n_0,n_1 $,所以能级的粒子总和为$ \large n_0+n_1 = N$。那么N个粒子的不同状态组合数记为$\large w $,且$ \large w $为:
$ \large w =C_{N}^{n_0} = \frac{N!}{n_0!n_1!} $
通过组合数计算一下熵,熵是来源热力学的概念,熵是衡量物质的混乱程度的量,通常和物质的状态有关,我们知道当物质的能量越高时混乱程度也越高,能量越低时混乱程度也越低,这和我们的常识认知是一致的,下面给出熵的定义:
$ \large S = K_Blogw $
其中 $\large K_B $是玻尔兹曼常数,取log就是熵的来源。
把$ \large w $带进上式的:
$ \large S = K_Blogw = K_B[log(N!) - log(n_0!)-log(n_1!)] \large \left ( 1 \right ) $
现在我给空间增加少了的能量 $\large \varepsilon $,此时封闭的空间的低能级的粒子 $ \large \varepsilon _0 $ 就会越变到高能级 $ \large \varepsilon _1 $,也就是说会有少量的$ \large n_0 $变为 $ \large n_1 $即:
$ \large n_0\rightarrow n_0-\alpha ,n_1\rightarrow n_1+\alpha $,其中 $ \large \alpha $是变化的粒子数,由此我们从新计算熵为:
$ \large S' = K_Blogw = K_B[log(N!) - log((n_0-\alpha )!)-log((n_1+\alpha )!)] \large \left ( 2 \right ) $
$ \large \left ( 2 \right ) - \left ( 1 \right ) $得到:
$ \large \Delta S = K_Blog\left ( \frac{n_0(n_0-1)....(n_0-\alpha ))}{(n_1+\alpha )....(n_1+1)} \right ) \large \left ( 3 \right ) $
我们知道上式的分子和分母项是一样多的,同时在封闭的空间中 $ \large n_0,n_1 $ 是足够大的,α是很小的,因此可以把(1)化简为:
$ \large \Delta S = K_Blog(\frac{n_0}{n_1}) \large \left ( 4 \right ) $
然而从热力学角度,熵的变化量和温度以及加入的能量 $ \large \varepsilon $有关(参考维基百科),因此有如下的公式;
$ \large \Delta S = \frac{\varepsilon }{T} \large \left ( 5 \right ) $
联立和 $\large \left ( 4 \right ) $ 和 $\large \left ( 5 \right ) $ 两两式的到:
$ \large K_Blog(\frac{n_0}{n_1}) = \frac{\varepsilon }{T} $
化简得到为:
$ \frac{n_0}{n_1} = e^{\frac{\varepsilon }{K_BT} } \left ( 6 \right ) $
从上式我们看到,不同能级的比值和能量、温度T、玻尔兹曼常数都有关系,且上式等式右边的指数和我们的退火算法很像,同时上式就称为玻尔兹曼分布。
好,从上面我们推倒了玻尔兹曼分布的来历。他是来源于热力学,大家通过我讲的简单型的可以完全理解了,掌握这些东西就够用了,如果对此感兴趣的同学可以看看完整版的玻尔兹曼分布,那里比这里稍微复杂一点,但是有这里的基础,看完整版的就会很容易了,好了,玻尔兹曼分布到此结束。
参考资料
